Нейросеть в 11 строчек на Python

Нейросеть в 11 строчек на Python

О чём статья

Лично я лучше всего обучаюсь при помощи небольшого работающего кода, с которым могу поиграться. В этом пособии мы научимся алгоритму обратного распространения ошибок на примере небольшой нейронной сети, реализованной на Python.

Дайте код!

Слишком сжато? Давайте разобьём его на более простые части.

Часть 1: Небольшая игрушечная нейросеть

Нейросеть, тренируемая через обратное распространение (backpropagation), пытается использовать входные данные для предсказания выходных.

Предположим, нам нужно предсказать, как будет выглядеть колонка «выход» на основе входных данных. Эту задачу можно было бы решить, подсчитав статистическое соответствие между ними. И мы бы увидели, что с выходными данными на 100% коррелирует левый столбец.

Обратное распространение, в самом простом случае, рассчитывает подобную статистику для создания модели. Давайте попробуем.

Нейросеть в два слоя

Переменные и их описания.

X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
“*” — поэлементное умножение – два вектора одного размера умножают соответствующие значения, и на выходе получается вектор такого же размера
“-” – поэлементное вычитание векторов
x.dot(y) – если x и y – это вектора, то на выходе получится скалярное произведение. Если это матрицы, то получится перемножение матриц. Если матрица только одна из них – это перемножение вектора и матрицы.

И это работает! Рекомендую перед прочтением объяснения поиграться немного с кодом и понять, как он работает. Он должен запускаться прямо как есть, в ipython notebook. С чем можно повозиться в коде:

• сравните l1 после первой итерации и после последней
• посмотрите на функцию nonlin.
• посмотрите, как меняется l1_error
• разберите строку 36 – основные секретные ингредиенты собраны тут (отмечена . )
• разберите строку 39 – вся сеть готовится именно к этой операции (отмечена . )

Разберём код по строчкам

Импортирует numpy, библиотеку линейной алгебры. Единственная наша зависимость.

Наша нелинейность. Конкретно эта функция создаёт «сигмоиду». Она ставит в соответствие любое число значению от 0 до 1 и преобразовывает числа в вероятности, а также имеет несколько других полезных для тренировки нейросетей свойств.

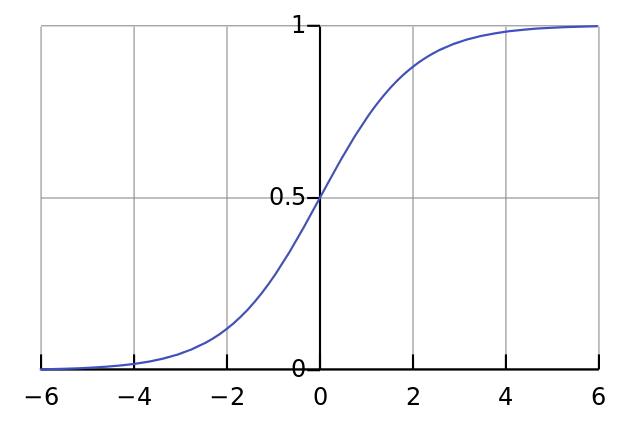
Эта функция также умеет выдавать производную сигмоиды (deriv=True). Это одно из её полезных свойств. Если выход функции – это переменная out, тогда производная будет out * (1-out). Эффективно.

Инициализация массива входных данных в виде numpy-матрицы. Каждая строка – тренировочный пример. Столбцы – это входные узлы. У нас получается 3 входных узла в сети и 4 тренировочных примера.

Инициализирует выходные данные. “.T” – функция переноса. После переноса у матрицы y есть 4 строки с одним столбцом. Как и в случае входных данных, каждая строка – это тренировочный пример, и каждый столбец (в нашем случае один) – выходной узел. У сети, получается, 3 входа и 1 выход.

Благодаря этому случайное распределение будет каждый раз одним и тем же. Это позволит нам проще отслеживать работу сети после внесения изменений в код.

Матрица весов сети. syn0 означает «synapse zero». Так как у нас всего два слоя, вход и выход, нам нужна одна матрица весов, которая их свяжет. Её размерность (3, 1), поскольку у нас есть 3 входа и 1 выход. Иными словами, l0 имеет размер 3, а l1 – 1. Поскольку мы связываем все узлы в l0 со всеми узлами l1, нам требуется матрица размерности (3, 1).

Заметьте, что она инициализируется случайным образом, и среднее значение равно нулю. За этим стоит достаточно сложная теория. Пока просто примем это как рекомендацию. Также заметим, что наша нейросеть – это и есть эта самая матрица. У нас есть «слои» l0 и l1, но они представляют собой временные значения, основанные на наборе данных. Мы их не храним. Всё обучение хранится в syn0.

Тут начинается основной код тренировки сети. Цикл с кодом повторяется многократно и оптимизирует сеть для набора данных.

Первый слой, l0, это просто данные. В X содержится 4 тренировочных примера. Мы обработаем их все и сразу – это называется групповой тренировкой [full batch]. Итого мы имеем 4 разных строки l0, но их можно представить себе как один тренировочный пример – на этом этапе это не имеет значения (можно было загрузить их 1000 или 10000 без всяких изменений в коде).

Это шаг предсказания. Мы позволяем сети попробовать предсказать вывод на основе ввода. Затем мы посмотрим, как это у неё получается, чтобы можно было подправить её в сторону улучшения.

В строке содержится два шага. Первый делает матричное перемножение l0 и syn0. Второй передаёт вывод через сигмоиду. Размерности у них следующие:

Матричные умножения требуют, чтобы в середине уравнения размерности совпадали. Итоговая матрица имеет количество строк, как у первой, а столбцов – как у второй.

Мы загрузили 4 тренировочных примера, и получили 4 догадки (матрица 4х1). Каждый вывод соответствует догадке сети для данного ввода.

Поскольку в l1 содержатся догадки, мы можем сравнить их разницу с реальностью, вычитая её l1 из правильного ответа y. l1_error – вектор из положительных и отрицательных чисел, характеризующий «промах» сети.

А вот и секретный ингредиент. Эту строку нужно разбирать по частям.

Первая часть: производная

l1 представляет три этих точки, а код выдаёт наклон линий, показанных ниже. Заметьте, что при больших значениях вроде x=2.0 (зелёная точка) и очень малые, вроде x=-1.0 (фиолетовая) линии имеют небольшой уклон. Самый большой угол у точки х=0 (голубая). Это имеет большое значение. Также отметьте, что все производные лежат в пределах от 0 до 1.

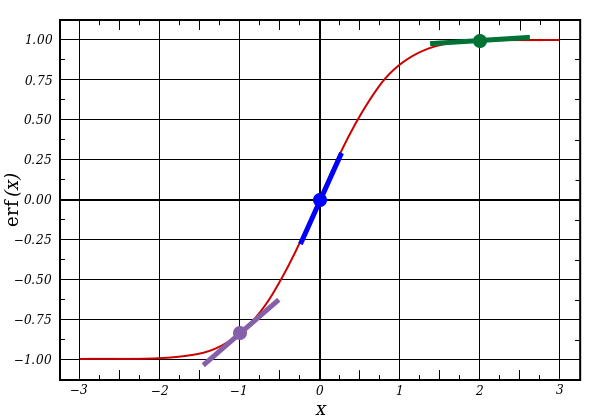
Полное выражение: производная, взвешенная по ошибкам

Математически существуют более точные способы, но в нашем случае подходит и этот. l1_error – это матрица (4,1). nonlin(l1,True) возвращает матрицу (4,1). Здесь мы поэлементно их перемножаем, и на выходе тоже получаем матрицу (4,1), l1_delta.

Умножая производные на ошибки, мы уменьшаем ошибки предсказаний, сделанных с высокой уверенностью. Если наклон линии был небольшим, то в сети содержится либо очень большое, либо очень малое значение. Если догадка в сети близка к нулю (х=0, у=0,5), то она не особенно уверенная. Мы обновляем эти неуверенные предсказания и оставляем в покое предсказания с высокой уверенностью, умножая их на величины, близкие к нулю.

Мы готовы к обновлению сети. Рассмотрим один тренировочный пример. В нём мы будем обновлять веса. Обновим крайний левый вес (9.5)

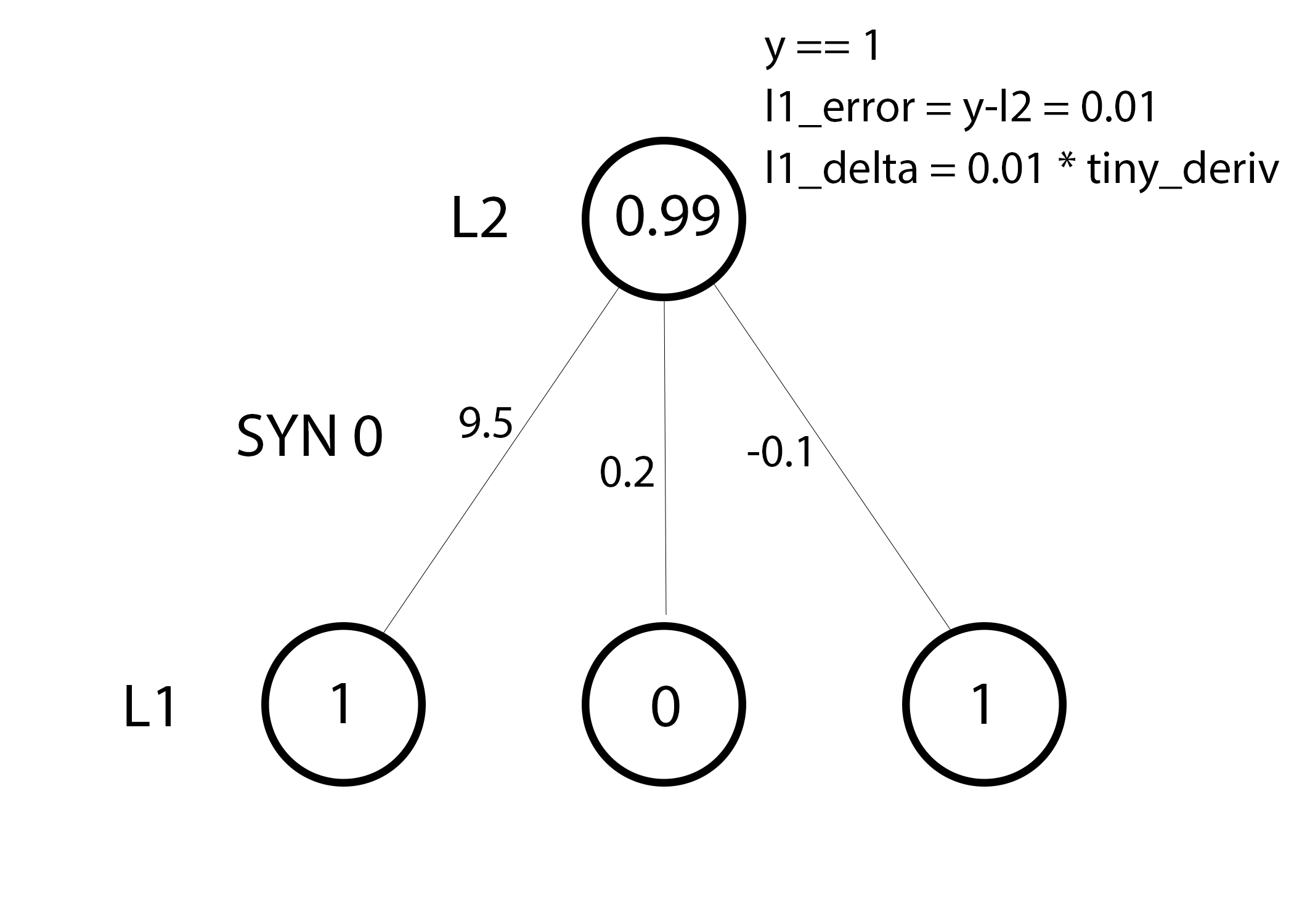
Для крайнего левого веса это будет 1.0 * l1_delta. Предположительно, это лишь незначительно увеличит 9.5. Почему? Поскольку предсказание было уже достаточно уверенным, и предсказания были практически правильными. Небольшая ошибка и небольшой наклон линии означает очень небольшое обновление.

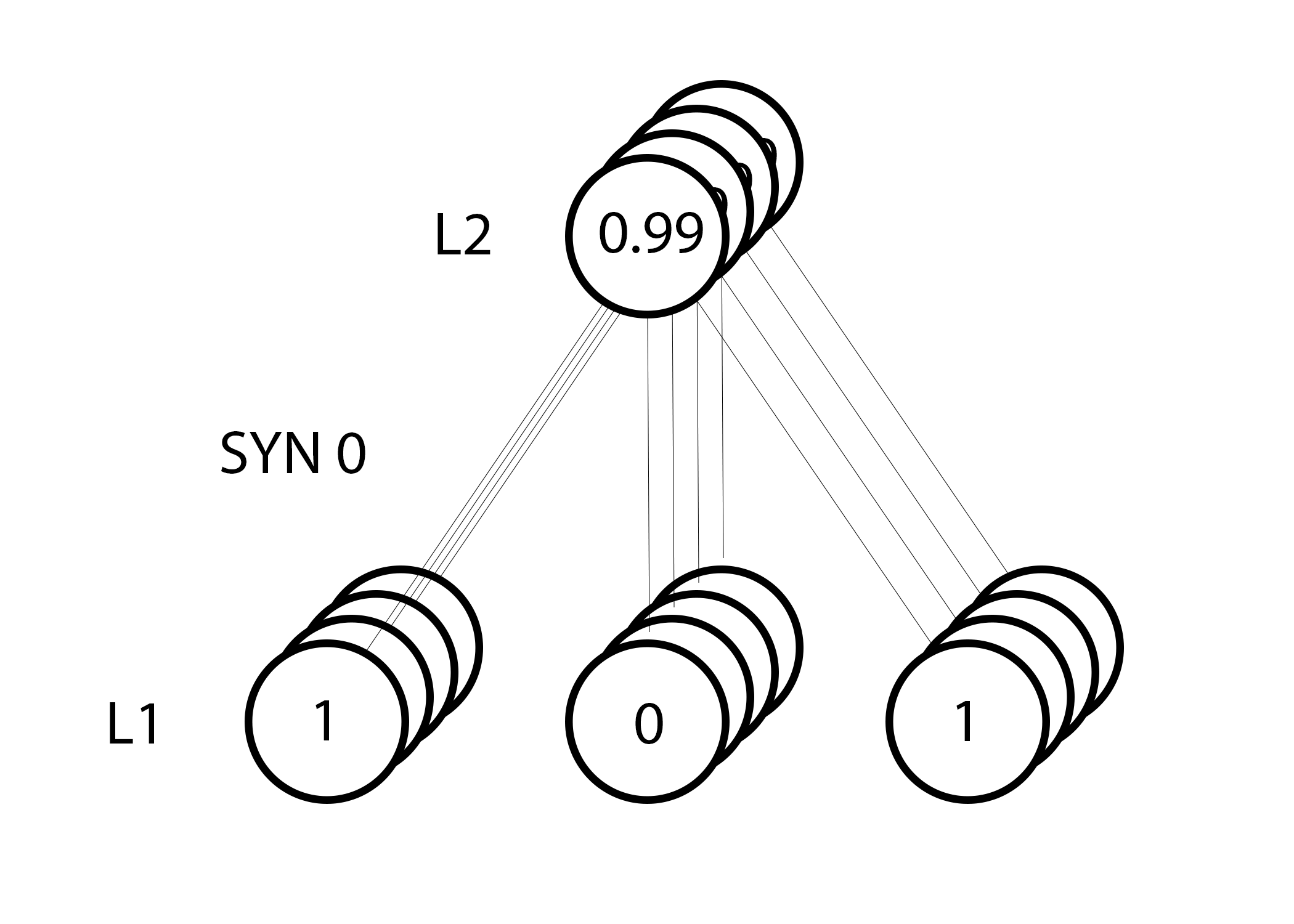
Но поскольку мы делаем групповую тренировку, указанный выше шаг мы повторяем для всех четырёх тренировочных примеров. Так что это выглядит очень похоже на изображение вверху. Так что же делает наша строчка? Она подсчитывает обновления весов для каждого веса, для каждого тренировочного примера, суммирует их и обновляет все веса – и всё одной строкой.

Понаблюдав за обновлением сети, вернёмся к нашим тренировочным данным. Когда и вход, и выход равны 1, мы увеличиваем вес между ними. Когда вход 1, а выход – 0, мы уменьшаем вес.

Таким образом, в наших четырёх тренировочных примерах ниже, вес первого входа по отношению к выходу будет постоянно увеличиваться или оставаться постоянным, а два других веса будут увеличиваться и уменьшаться в зависимости от примеров. Этот эффект и способствует обучению сети на основе корреляций входных и выходных данных.

Часть 2: задачка посложнее

Попробуем предсказать выходные данные на основе трёх входных столбцов данных. Ни один из входных столбцов не коррелирует на 100% с выходным. Третий столбец вообще ни с чем не связан, поскольку в нём всю дорогу содержатся единицы. Однако и тут можно увидеть схему – если в одном из двух первых столбцов (но не в обоих сразу) содержится 1, то результат также будет равен 1.

Это нелинейная схема, поскольку прямого соответствия столбцов один к одному не существует. Соответствие строится на комбинации входных данных, столбцов 1 и 2.

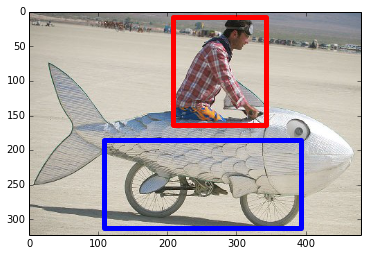
Интересно, что распознавание образов является очень похожей задачей. Если у вас есть 100 картинок одинакового размера, на которых изображены велосипеды и курительные трубки, присутствие на них определённых пикселей в определённых местах не коррелирует напрямую с наличием на изображении велосипеда или трубки. Статистически их цвет может казаться случайным. Но некоторые комбинации пикселей не случайны – те, что формируют изображение велосипеда (или трубки).

Стратегия

Чтобы скомбинировать пиксели в нечто, у чего может появиться однозначное соответствие с выходными данными, нужно добавить ещё один слой. Первый слой комбинирует вход, второй назначает соответствие выходу, используя в качестве входных данных выходные данные первого слоя. Обратите внимание на таблицу.

Случайным образом назначив веса, мы получим скрытые значения для слоя №1. Интересно, что у второго столбца скрытых весов уже есть небольшая корреляция с выходом. Не идеальная, но есть. И это тоже является важной частью процесса тренировки сети. Тренировка будет только усиливать эту корреляцию. Она будет обновлять syn1, чтобы назначить её соответствие выходным данным, и syn0, чтобы лучше получать данные со входа.

Нейросеть в три слоя

Переменные и их описания

X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
l2 – финальный слой, это наша гипотеза. По мере тренировки должен приближаться к правильному ответу
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
syn1 – второй слой весов, Synapse 1, объединяет l1 с l2.
l2_error – промах сети в количественном выражении
l2_delta – ошибка сети, в зависимости от уверенности предсказания. Почти совпадает с ошибкой, за исключением уверенных предсказаний
l1_error – взвешивая l2_delta весами из syn1, мы подсчитываем ошибку в среднем/скрытом слое
l1_delta – ошибки сети из l1, масштабируемые по увеернности предсказаний. Почти совпадает с l1_error, за исключением уверенных предсказаний

Код должен быть достаточно понятным – это просто предыдущая реализация сети, сложенная в два слоя один над другим. Выход первого слоя l1 – это вход второго слоя. Что-то новое есть лишь в следующей строке.

Использует ошибки, взвешенные по уверенности предсказаний из l2, чтобы подсчитать ошибку для l1. Получаем, можно сказать, ошибку, взвешенную по вкладам – мы подсчитываем, какой вклад в ошибки в l2 вносят значения в узлах l1. Этот шаг и называется обратным распространением ошибок. Затем мы обновляем syn0, используя тот же алгоритм, что и в варианте с нейросетью из двух слоёв.

Что такое нейронная сеть?

Большинство статей по нейронным сетям при их описании проводят параллели с мозгом. Мне проще описать нейронные сети как математическую функцию, которая отображает заданный вход в желаемый результат, не вникая в подробности.

Нейронные сети состоят из следующих компонентов:

• входной слой, x
• произвольное количество скрытых слоев
• выходной слой, ŷ
• набор весов и смещений между каждым слоем Wи b
• выбор функции активации для каждого скрытого слоя σ; в этой работе мы будем использовать функцию активации Sigmoid

На приведенной ниже диаграмме показана архитектура двухслойной нейронной сети (обратите внимание, что входной уровень обычно исключается при подсчете количества слоев в нейронной сети).

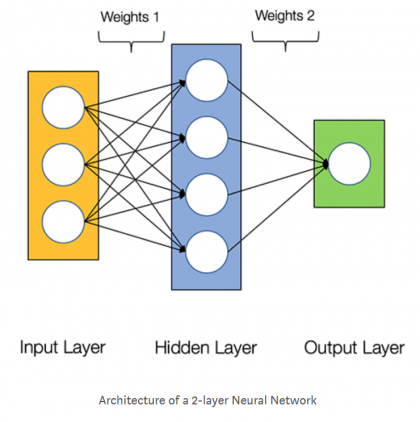
Создание класса Neural Network на Python выглядит просто:

Подготовка функций и переменных

Библиотека NumPy широко используется для расчетов в нейросети, а библиотека Pandas дает мне удобный способ импортировать данные обучения из файла Excel.

Как вы уже знаете, для активации мы используем функцию логистической сигмоиды. Для расчета значений постактивации нам нужна сама логистическая функция, а для обратного распространения необходима производная логистической функции.

Затем мы выбираем скорость обучения, размерность входного слоя, размерность скрытого слоя и количество эпох. Для реальных нейронных сетей важно обучение в течение нескольких эпох, потому что это позволяет вам извлечь больше информации из ваших обучающих данных. Когда вы генерируете обучающие данные в Excel, вам не нужно запускать несколько эпох, потому что вы можете легко создать больше обучающих выборок.

Функция np.random.uniform() заполняет наши две матрицы весов случайными значениями от –1 до +1 (обратите внимание, что матрица весов между скрытым и выходным слоями на самом деле представляет собой просто массив, поскольку у нас только один выходной узел). Оператор np.random.seed(1) приводит к тому, что случайные значения становятся одинаковыми при каждом запуске программы. Начальные значения весов могут оказать существенное влияние на конечную производительность обученной сети, поэтому, если вы пытаетесь оценить, как другие переменные улучшают или ухудшают производительность, вы можете раскомментировать эту инструкцию и тем самым устранить влияние случайной инициализации весовых коэффициентов.

И в конце я создаю пустые массивы для значений преактивации и постактивации в скрытом слое.

Формула корректировки весов

Во время тренировочного цикла (он изображен на рисунке 3) мы постоянно корректируем веса. Но на сколько? Для того, чтобы вычислить это, мы воспользуемся следующей формулой:

Давайте поймем почему формула имеет такой вид. Сначала нам нужно учесть то, что мы хотим скорректировать вес пропорционально размеру ошибки. Далее ошибка умножается на значение, поданное на вход нейрона, что, в нашем случае, 0 или 1. Если на вход был подан 0, то вес не корректируется. И в конце выражение умножается на градиент сигмоиды. Разберемся в последнем шаге по порядку:

1. Мы использовали сигмоиду для того, чтобы посчитать выход нейрона.
2. Если на выходе мы получаем большое положительное или отрицательное число, то это значит, что нейрон был весьма уверен в том или ином решении.
3. На рисунке 4 мы можем увидеть, что при больших значениях переменной градиент принимает маленькие значения.
4. Если нейрон уверен в том, что заданный вес верен, то мы не хотим сильно корректировать его. Умножение на градиент сигмоиды позволяет добиться такого эффекта.

Градиент сигмоиды может быть найден по следующей формуле:

Таким образом, подставляя второе уравнение в первое, конечная формула для корректировки весов будет выглядеть следующим образом:

Существуют и другие формулы, которые позволяют нейрону обучаться быстрее, но преимущество этой формулы в том, что она достаточно проста для понимания.

Читайте также

Программа курса Введение в нейронные сети на Python

1. Простейшие нейронные сети
   • Теоретическая часть: основные понятия; классификация задач, решаемых с помощью методов машинного обучения; виды данных, понятие датасета; полносвязные нейронные сети.
   • Практическая часть: первичный анализ датасета, предобработка данных, построение полносвязной нейронной сети.
2. Математические основы нейронных сетей
   • Теоретическая часть: метрики качества работы нейронной сети, градиентный спуск, алгоритм обратного распространения ошибки, эффект переобучения.
   • Практическая часть: тонкая настройка нейронной сети на примере задачи классификации изображений.
3. Свёрточные нейронные сети
   • Теоретическая часть: параметры сверточных нейронных сетей, предобученные нейронные сети.
   • Практическая часть: использование предобученных нейронных сетей на примере задачи классификации изображений.
4. Решение кейса: “Классификация изображений”
   • Теоретическая часть: построение набора данных, фильтрация и предобработка данных.
   • Практическая часть: решение кейса.
5. Использование нейронных сетей вproduction
   • Теоретическая часть: сериализация/десериализация объектов в Python, фреймворк Flask.
   • Практическая часть: создание веб-сервиса на фреймворке Flask.

Изучаем нейронные сети за четыре шага

В этот раз я решил изучить нейронные сети. Базовые навыки в этом вопросе я смог получить за лето и осень 2015 года. Под базовыми навыками я имею в виду, что могу сам создать простую нейронную сеть с нуля. Примеры можете найти в моих репозиториях на GitHub. В этой статье я дам несколько разъяснений и поделюсь ресурсами, которые могут пригодиться вам для изучения.

Шаг 1. Нейроны и метод прямого распространения

Так что же такое «нейронная сеть»? Давайте подождём с этим и сперва разберёмся с одним нейроном.

Нейрон похож на функцию: он принимает на вход несколько значений и возвращает одно.

Круг ниже обозначает искусственный нейрон. Он получает 5 и возвращает 1. Ввод — это сумма трёх соединённых с нейроном синапсов (три стрелки слева).

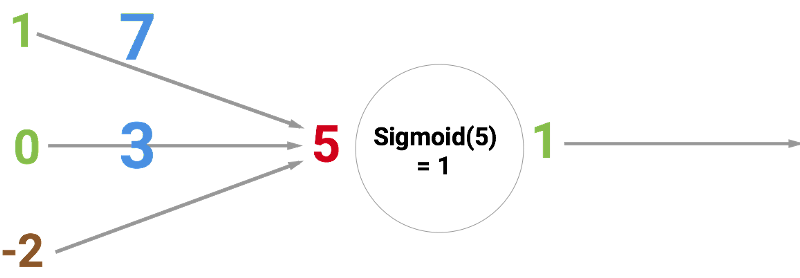
В левой части картинки мы видим 2 входных значения (зелёного цвета) и смещение (выделено коричневым цветом).

«Ситиконсалт», удалённо, 200 000 ₽

Входные данные могут быть численными представлениями двух разных свойств. Например, при создании спам-фильтра они могли бы означать наличие более чем одного слова, написанного ЗАГЛАВНЫМИ БУКВАМИ, и наличие слова «виагра».

Входные значения умножаются на свои так называемые «веса», 7 и 3 (выделено синим).

Теперь мы складываем полученные значения со смещением и получаем число, в нашем случае 5 (выделено красным). Это — ввод нашего искусственного нейрона.

Потом нейрон производит какое-то вычисление и выдает выходное значение. Мы получили 1, т.к. округлённое значение сигмоиды в точке 5 равно 1 (более подробно об этой функции поговорим позже).

Если бы это был спам-фильтр, факт вывода 1 означал бы то, что текст был помечен нейроном как спам.

Иллюстрация нейронной сети с Википедии.

Если вы объедините эти нейроны, то получите прямо распространяющуюся нейронную сеть — процесс идёт от ввода к выводу, через нейроны, соединённые синапсами, как на картинке слева.

Я очень рекомендую посмотреть серию видео от Welch Labs для улучшения понимания процесса.

Шаг 2. Сигмоида

После того, как вы посмотрели уроки от Welch Labs, хорошей идеей было бы ознакомиться с четвертой неделей курса по машинному обучению от Coursera, посвящённой нейронным сетям — она поможет разобраться в принципах их работы. Курс сильно углубляется в математику и основан на Octave, а я предпочитаю Python. Из-за этого я пропустил упражнения и почерпнул все необходимые знания из видео.

Сигмоида просто-напросто отображает ваше значение (по горизонтальной оси) на отрезок от 0 до 1.

Первоочередной задачей для меня стало изучение сигмоиды, так как она фигурировала во многих аспектах нейронных сетей. Что-то о ней я уже знал из третьей недели вышеупомянутого курса, поэтому я пересмотрел видео оттуда.

Но на одних видео далеко не уедешь. Для полного понимания я решил закодить её самостоятельно. Поэтому я начал писать реализацию алгоритма логистической регрессии (который использует сигмоиду).

Это заняло целый день, и вряд ли результат получился удовлетворительным. Но это неважно, ведь я разобрался, как всё работает. Код можно увидеть здесь.

Вам необязательно делать это самим, поскольку тут требуются специальные знания — главное, чтобы вы поняли, как устроена сигмоида.

Шаг 3. Метод обратного распространения ошибки

Понять принцип работы нейронной сети от ввода до вывода не так уж и сложно. Гораздо сложнее понять, как нейронная сеть обучается на наборах данных. Использованный мной принцип называется методом обратного распространения ошибки.

Вкратце: вы оцениваете, насколько сеть ошиблась, и изменяете вес входных значений (синие числа на первой картинке).

Процесс идёт от конца к началу, так как мы начинаем с конца сети (смотрим, насколько отклоняется от истины догадка сети) и двигаемся назад, изменяя по пути веса, пока не дойдём до ввода. Для вычисления всего этого вручную потребуются знания матанализа. Khan Academy предоставляет хорошие курсы по матанализу, но я изучал его в университете. Также можно не заморачиваться и воспользоваться библиотеками, которые посчитают весь матан за вас.

Скриншот из руководства Мэтта Мазура по методу обратного распространения ошибки.

Вот три источника, которые помогли мне разобраться в этом методе:

В процессе прочтения первых двух статей вам обязательно нужно кодить самим, это поможет вам в дальнейшем. Да и вообще, в нейронных сетях нельзя как следует разобраться, если пренебречь практикой. Третья статья тоже классная, но это скорее энциклопедия, поскольку она размером с целую книгу. Она содержит подробные объяснения всех важных принципов работы нейронных сетей. Эти статьи также помогут вам изучить такие понятия, как функция стоимости и градиентный спуск.

Шаг 4. Создание своей нейронной сети

При прочтении различных статей и руководств вы так или иначе будете писать маленькие нейронные сети. Рекомендую именно так и делать, поскольку это — очень эффективный метод обучения.

Ещё одной полезной статьёй оказалась A Neural Network in 11 lines of Python от IAmTrask. В ней содержится удивительное количество знаний, сжатых до 11 строк кода.

Скриншот руководства от IAmTrask

После прочтения этой статьи вам следует написать реализацию всех примеров самостоятельно. Это поможет вам закрыть дыры в знаниях, а когда у вас получится, вы почувствуете, будто обрели суперсилу.

Поскольку в примерах частенько встречаются реализации, использующие векторные вычисления, я рекомендую пройти курс по линейной алгебре от Coursera.

После этого можно ознакомиться с руководством Wild ML от Denny Britz, в котором разбираются нейронные сети посложнее.

Скриншот из руководства WildML

Теперь вы можете попробовать написать свою собственную нейронную сеть или поэкспериментировать с уже написанными. Очень забавно найти интересующий вас набор данных и проверить различные предположения при помощи ваших сетей.

Для поиска хороших наборов данных можете посетить мой сайт Datasets.co и выбрать там подходящий.

Так или иначе, теперь вам лучше начать свои эксперименты, чем слушать мои советы. Лично я сейчас изучаю Python-библиотеки для программирования нейронных сетей, такие как Theano, Lasagne и nolearn.

Как обучить глубокую нейронную сеть с помощью 7 строк кода

Сущность машинного обучения – это распознавание закономерностей в данных. Для этого требуются три компонента: данные, программное обеспечение и математика. Вы спросите, что можно сделать с помощью 7 строк кода? Отвечу вам: очень многое.

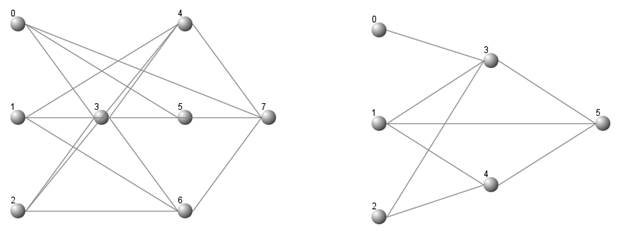
Уложиться в 7 строк кода при решении задачи глубокого обучения нам позволит применение библиотек, реализующих слои абстракции. Подобные библиотеки называются «фреймворками». Сегодня нашими инструментами будут TensorFlow и TFLearn.

Абстракция – это неотъемлемое свойство программного обеспечения. Например, приложение, в котором вы сейчас читаете эту статью, является слоем абстракции над вашей операционной системой, умеющей читать файлы, передавать данные и др. Далее следуют функции более низкого уровня. Наконец, существует код уровня процессора, который оперирует битами, – здесь работает «голое железо».

Фреймворк – это слой абстракции

Краткость нашего кода будет обеспечена с помощью фреймворка TFLearn, являющегося надстройкой над TensorFlow, в свою очередь являющегося надстройкой над Python. Как обычно, чтобы упростить организацию кода, мы будем работать в блокноте IPython.

Начнем с самого начала

В статье «Как работают нейронные сети» («How Neural Networks Work») была создана нейронная сеть на Python без использования фреймворков, и продемонстрирован процесс обучения, в рамках которого нейронная сеть обучается находить закономерности в данных. Мы намеренно использовали очень простые «игрушечные данные», закономерности в которых видны невооруженным глазом.

Блокнот, содержащий код этого проекта, реализующего «нулевой уровень абстракции», находится здесь. Каждая математическая операция в модели подробно описана.

Усовершенствовав эту модель путем реализации 2 скрытых слоев и градиентного спуска (gradient descent) (аналогично проекту для анализа текста), мы получаем около 80 строк кода, опять же без применения фреймворков. Эта нейронная сеть является глубокой, поскольку содержит скрытые слои.

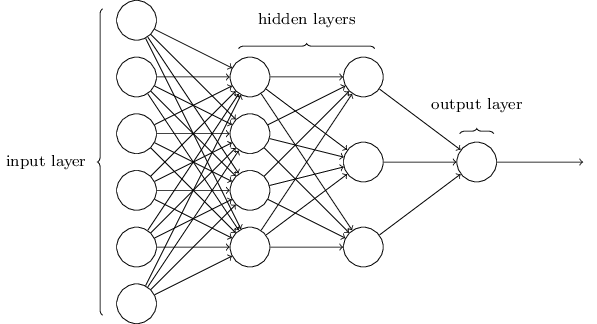
Нейронная сеть с двумя скрытыми слоями

Логика нашей модели достаточно проста, но ее реализация является трудоемкой. Большая часть кода относится к процессу обучения:

Этот код отлично работал. Затем мы абстрагировали его с помощью фреймворка.

Абстрагируем модель с помощью TensorFlow

В статье «Разоблачение TensorFlow» («TensorFlow demystified») описанная выше сеть была реализована с применением TensorFlow. Еще раз была продемонстрирована способность модели выявлять закономерности в данных.

Абстрагирование позволило существенно упростить код. Например, реализация градиентного спуска и функции потерь сократилась до 2 строк.

Весь код можно найти здесь.

Определение модели также упростилось. Математические операции и распространенные функции (например, сигмоида) инкапсулированы во фреймворке.

Впрочем, если представить себе сложную нейронную сеть, такую как AlexNet, ее реализация даже с применением TensorFlow будет громоздкой.

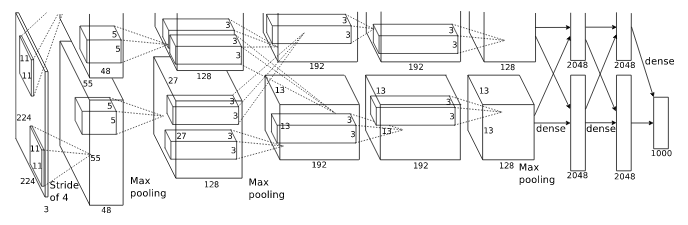
Еще один слой абстракции

Поскольку код по-прежнему является достаточно многословным, мы задействуем еще один слой абстракции, представленный в библиотеке TFLearn. Этот инструмент описывается следующим образом:

TFLearn: библиотека глубокого обучения, реализующая высокоуровневый API для TensorFlow.

Термин «высокоуровневый API» говорит о том, что данная библиотека дает нам более высокий уровень абстракции, что нам и нужно. Теперь наша многослойная нейронная сеть может быть реализована с помощью 7 строк кода.

Просто великолепно: 5 строк, чтобы задать архитектуру сети (входной слой + 2 скрытых слоя + выходной слой + регрессия), и 2 строки, чтобы обучить ее.

Полный код находится здесь.

Давайте рассмотрим эту реализацию подробно. Вы увидите, что данные и логика идентичны рассмотренной выше реализации, где применялся лишь TensorFlow.

Устанавливаем TFLearn

Убедитесь, что у вас установлен TensorFlow версии не менее 1.0.x, поскольку TFLearn не будет работать с более ранней версией. Выведем версию:

В результате мы должны получить примерно следующее: ‘1.0.1’

Чтобы установить (обновить) TensorFlow и TFLearn выполним следующую команду:

Данные

Далее мы создаем наши «игрушечные» данные, те же самые, что были использованы в рассмотренной выше реализации, где применялся лишь TensorFlow. Обратите внимание, больше нет необходимости формировать валидационный набор данных для использования в процессе обучения, поскольку TFLearn может сделать это за нас.

Великолепная семерка

И, наконец, код, реализующий непосредственно глубокое обучение:

Первые 5 строк задают архитектуру нашей нейронной сети с помощью следующих функций: tflearn.input_data, tflearn.fully_connected, tflearn.regression. Входные данные имеют 5 признаков, мы используем 32 нейрона в каждом скрытом слое, а на выходе получаем вероятности 2 классов.

Далее мы создаем глубокую нейронную сеть на основе заданной архитектуры с помощью tflearn.DNN. Мы используем параметр tensorboard_dir, чтобы задать путь для сохранения журнала.

И, наконец, мы обучаем нашу нейронную сеть. Следует отметить удобный интерфейс отображения метрик в процессе обучения. Далее мы можем изменить значение параметра n_epoch, чтобы оценить его влияние на точность (accuracy).

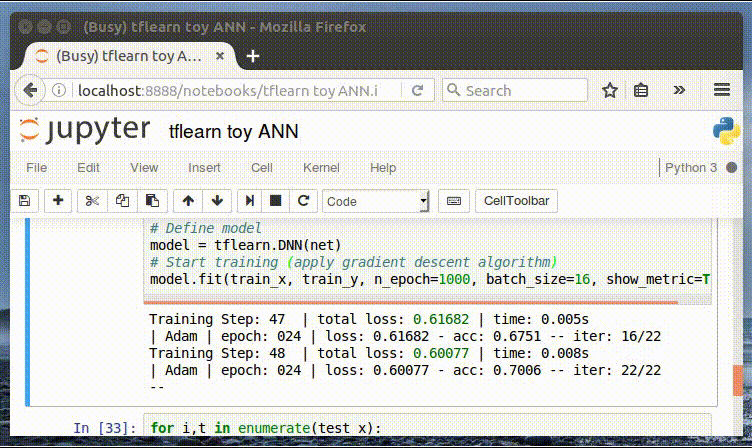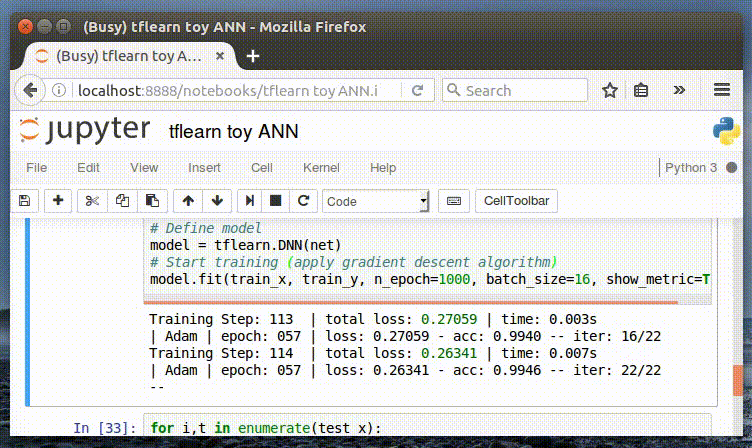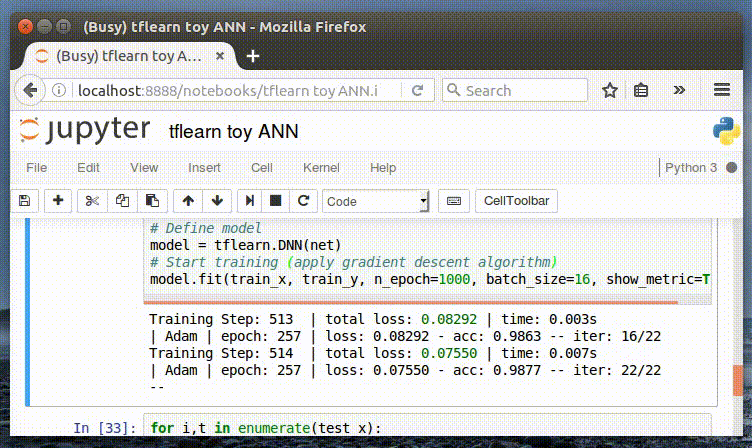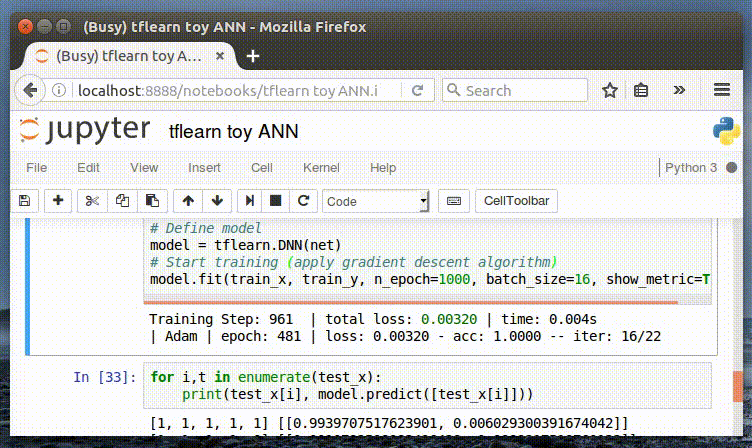
Интерактивное отображение метрик в процессе обучения

Training Step: 1999 | total loss: 0.01591 | time: 0.003s

| Adam | epoch: 1000 | loss: 0.01591 — acc: 0.9997 — iter: 16/22

Training Step: 2000 | total loss: 0.01561 | time: 0.006s

| Adam | epoch: 1000 | loss: 0.01561 — acc: 0.9997 — iter: 22/22

Тестируем модель

Теперь мы можем использовать нашу нейронную сеть для прогнозирования. Перед началом обучения обязательно необходимо убедиться в том, что в наборе обучающих данных нет примеров, на которых мы хотим протестировать модель, иначе модель будет «жульничать». Строки, содержащие примеры для тестирования, можно просто закомментировать.

Наша модель правильно распознает закономерность [1, _, _, _, 1], давая на выходе [1, 0].

Для удобства при многократной работе с блокнотом мы сбрасываем граф модели, добавив следующие 2 строки непосредственно перед кодом модели:

Благодаря абстрагированию с помощью фреймворка, мы больше не должны тратить время на кропотливую реализацию и можем сосредоточиться на подготовке данных и прогнозировании.

TensorBoard

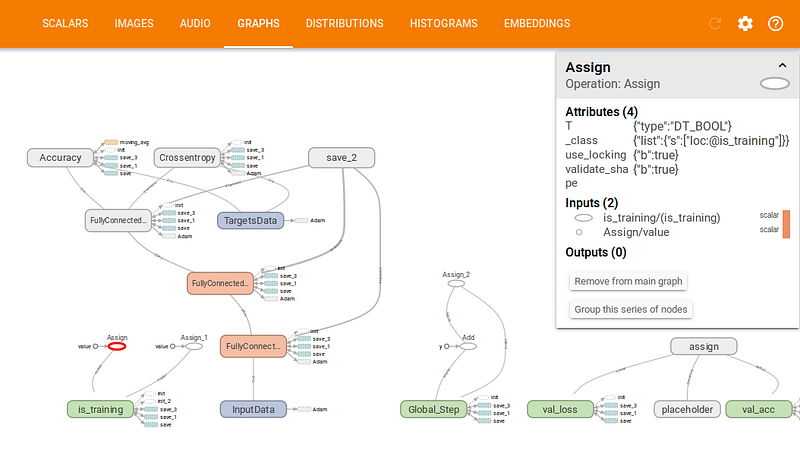
TFLearn автоматически передает данные в TensorBoard – инструмент визуализации TensorFlow. В tflearn.DNN мы задали путь для журнала, теперь мы можем на него взглянуть:

На рисунке ниже представлен граф нашей модели:

Также мы можем увидеть графики функции потерь и точности:

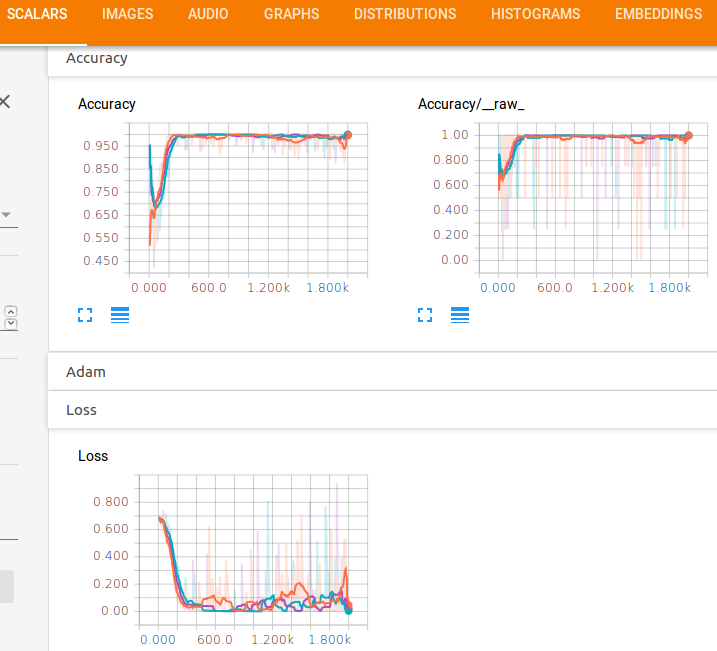
Очевидно, что нам не требуется такое большое количество эпох для достижения хорошей точности.

Другие примеры

Теперь давайте посмотрим, как с помощью TFLearn можно реализовать рекуррентную LSTM-сеть (LSTM recurrent neural network). Такие сети обычно используются в тех случаях, когда необходимо обучить модель на последовательности данных с реализацией памяти. В данном случае мы имеем другую архитектуру с применением функции tflearn.lstm, но при этом базовая концепция остается все той же.

Полный код примера доступен здесь.

В качестве еще одного примера давайте рассмотрим реализацию сверточной нейронной сети (convolutional neural network) с помощью TFLearn. Данный тип сетей применяется для распознавания изображений. Как и в других примерах, мы просто задаем последовательность математических операций, определяющих архитектуру сети, а затем обучаем ее.

Полный код примера доступен здесь.

Начиная изучение нейронных сетей, полезно разобраться в коде, написанном без использования фреймворков. Этот подход позволяет приобрести хорошее понимание внутренних процессов без «черных ящиков». Затем мы можем приступать к применению фреймворков, которые позволяют существенно сократить объем кода.

Фреймворки глубокого обучения упрощают нашу работу, инкапсулируя функции более низкого уровня. По мере развития фреймворков, мы автоматически наследуем все усовершенствования, получая в свое распоряжение мощные функции высокого уровня.

Задача классификации

Теперь рассмотрим нейронную сеть на примере задачи классификации. Нейронные сети способны решать множество задач, мы же рассмотрим наиболее простую из них – задачу классификации. Суть задачи состоит в классификации объекта к определенной группе. Например, мы рисуем число 0, а нейронка должна понять что это за число. Другой пример, мы указываем характеристики автомобиля, а нейронка исходя из описания классифицирует машину и говорит её название.

В любой нейронке есть входные сигналы. Это те характеристики что мы с вами указываем, например, описание автомобиля. На основе этих данных нейронная сеть должна понять какой это автомобиль. Чтобы сделать решение она должна взвесить предоставленные данные и для этого используются, так называемые, весы. Это дополнительные числа, на которые в последствии будут умножены входные сигналы.

После умножения все данные суммируют, добавляется число корреляции и далее результат сравнивают с неким числом. Если итог более числа 0, то можно предположить, что машина, к примеру, Mercedes, а если менее 0, то это будет, например, BMW.

Мы рассмотрели работу лишь одного нейрона. Обычно для задач используется сеть нейронов, то есть объединение нескольких нейронов, где каждый из них решает какую-либо свою небольшую задачу.

Первый слой нейронов может решить несколько своих небольших задач и дать нам ответы. Далее на основе ответов формируется второй слой нейронов, скрытый слой, который также решает задачи и дает ответы. Таких слоев может быть множество и чем их больше, тем сложнее нейронная сеть. В конечном результате мы получаем множество взвешенных решений и на их основе спокойно можем вынести вердикт. В нашем примере нейронка могла бы сказать к какой марке относиться автомобиль.

Что дальше?

К счастью для нас, наше путешествие еще не закончено. Там ещемногоузнать о нейронных сетях и глубоком обучении. Например:

• Какие другиефункция активациимы можем использовать помимо функции Sigmoid?
• С помощьюскорость обученияпри обучении нейронной сети
• С помощьюизвилиныдля задач классификации изображений

Я скоро напишу больше на эти темы, так что следите за мной на Medium и следите за ними!