Изучаем нейронные сети за четыре шага

Изучаем нейронные сети за четыре шага

В этот раз я решил изучить нейронные сети. Базовые навыки в этом вопросе я смог получить за лето и осень 2015 года. Под базовыми навыками я имею в виду, что могу сам создать простую нейронную сеть с нуля. Примеры можете найти в моих репозиториях на GitHub. В этой статье я дам несколько разъяснений и поделюсь ресурсами, которые могут пригодиться вам для изучения.

Шаг 1. Нейроны и метод прямого распространения

Так что же такое «нейронная сеть»? Давайте подождём с этим и сперва разберёмся с одним нейроном.

Нейрон похож на функцию: он принимает на вход несколько значений и возвращает одно.

Круг ниже обозначает искусственный нейрон. Он получает 5 и возвращает 1. Ввод — это сумма трёх соединённых с нейроном синапсов (три стрелки слева).

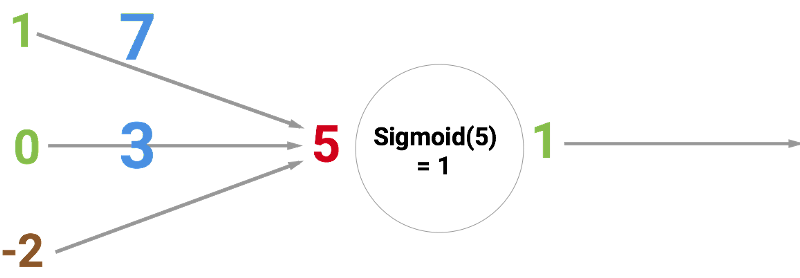
В левой части картинки мы видим 2 входных значения (зелёного цвета) и смещение (выделено коричневым цветом).

«Ситиконсалт», удалённо, 200 000 ₽

Входные данные могут быть численными представлениями двух разных свойств. Например, при создании спам-фильтра они могли бы означать наличие более чем одного слова, написанного ЗАГЛАВНЫМИ БУКВАМИ, и наличие слова «виагра».

Входные значения умножаются на свои так называемые «веса», 7 и 3 (выделено синим).

Теперь мы складываем полученные значения со смещением и получаем число, в нашем случае 5 (выделено красным). Это — ввод нашего искусственного нейрона.

Потом нейрон производит какое-то вычисление и выдает выходное значение. Мы получили 1, т.к. округлённое значение сигмоиды в точке 5 равно 1 (более подробно об этой функции поговорим позже).

Если бы это был спам-фильтр, факт вывода 1 означал бы то, что текст был помечен нейроном как спам.

Иллюстрация нейронной сети с Википедии.

Если вы объедините эти нейроны, то получите прямо распространяющуюся нейронную сеть — процесс идёт от ввода к выводу, через нейроны, соединённые синапсами, как на картинке слева.

Я очень рекомендую посмотреть серию видео от Welch Labs для улучшения понимания процесса.

Шаг 2. Сигмоида

После того, как вы посмотрели уроки от Welch Labs, хорошей идеей было бы ознакомиться с четвертой неделей курса по машинному обучению от Coursera, посвящённой нейронным сетям — она поможет разобраться в принципах их работы. Курс сильно углубляется в математику и основан на Octave, а я предпочитаю Python. Из-за этого я пропустил упражнения и почерпнул все необходимые знания из видео.

Сигмоида просто-напросто отображает ваше значение (по горизонтальной оси) на отрезок от 0 до 1.

Первоочередной задачей для меня стало изучение сигмоиды, так как она фигурировала во многих аспектах нейронных сетей. Что-то о ней я уже знал из третьей недели вышеупомянутого курса, поэтому я пересмотрел видео оттуда.

Но на одних видео далеко не уедешь. Для полного понимания я решил закодить её самостоятельно. Поэтому я начал писать реализацию алгоритма логистической регрессии (который использует сигмоиду).

Это заняло целый день, и вряд ли результат получился удовлетворительным. Но это неважно, ведь я разобрался, как всё работает. Код можно увидеть здесь.

Вам необязательно делать это самим, поскольку тут требуются специальные знания — главное, чтобы вы поняли, как устроена сигмоида.

Шаг 3. Метод обратного распространения ошибки

Понять принцип работы нейронной сети от ввода до вывода не так уж и сложно. Гораздо сложнее понять, как нейронная сеть обучается на наборах данных. Использованный мной принцип называется методом обратного распространения ошибки.

Вкратце: вы оцениваете, насколько сеть ошиблась, и изменяете вес входных значений (синие числа на первой картинке).

Процесс идёт от конца к началу, так как мы начинаем с конца сети (смотрим, насколько отклоняется от истины догадка сети) и двигаемся назад, изменяя по пути веса, пока не дойдём до ввода. Для вычисления всего этого вручную потребуются знания матанализа. Khan Academy предоставляет хорошие курсы по матанализу, но я изучал его в университете. Также можно не заморачиваться и воспользоваться библиотеками, которые посчитают весь матан за вас.

Скриншот из руководства Мэтта Мазура по методу обратного распространения ошибки.

Вот три источника, которые помогли мне разобраться в этом методе:

В процессе прочтения первых двух статей вам обязательно нужно кодить самим, это поможет вам в дальнейшем. Да и вообще, в нейронных сетях нельзя как следует разобраться, если пренебречь практикой. Третья статья тоже классная, но это скорее энциклопедия, поскольку она размером с целую книгу. Она содержит подробные объяснения всех важных принципов работы нейронных сетей. Эти статьи также помогут вам изучить такие понятия, как функция стоимости и градиентный спуск.

Шаг 4. Создание своей нейронной сети

При прочтении различных статей и руководств вы так или иначе будете писать маленькие нейронные сети. Рекомендую именно так и делать, поскольку это — очень эффективный метод обучения.

Ещё одной полезной статьёй оказалась A Neural Network in 11 lines of Python от IAmTrask. В ней содержится удивительное количество знаний, сжатых до 11 строк кода.

Скриншот руководства от IAmTrask

После прочтения этой статьи вам следует написать реализацию всех примеров самостоятельно. Это поможет вам закрыть дыры в знаниях, а когда у вас получится, вы почувствуете, будто обрели суперсилу.

Поскольку в примерах частенько встречаются реализации, использующие векторные вычисления, я рекомендую пройти курс по линейной алгебре от Coursera.

После этого можно ознакомиться с руководством Wild ML от Denny Britz, в котором разбираются нейронные сети посложнее.

Скриншот из руководства WildML

Теперь вы можете попробовать написать свою собственную нейронную сеть или поэкспериментировать с уже написанными. Очень забавно найти интересующий вас набор данных и проверить различные предположения при помощи ваших сетей.

Для поиска хороших наборов данных можете посетить мой сайт Datasets.co и выбрать там подходящий.

Так или иначе, теперь вам лучше начать свои эксперименты, чем слушать мои советы. Лично я сейчас изучаю Python-библиотеки для программирования нейронных сетей, такие как Theano, Lasagne и nolearn.

Иерархия классов

Существует три базовых класса TNeuron, TLayer, TNeuralNet. Все остальные являются производными от них. На рис.1 приведена иерархия классов, сплошными линиями показано наследование (стрелкой указан потомок), пунктирными в каких классах они используются.

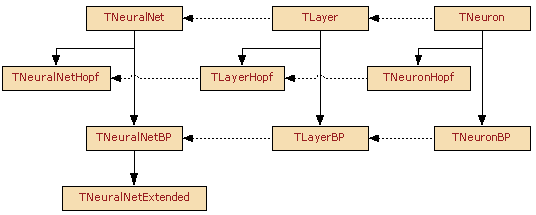
TNeuron является базовым классом для нейронов, несет всю основную функциональность, имеет индексированное свойство Weights, представляющее собой весовые коэффициенты (синапсы), свойство Output, которое является выходом нейрона (результатом вычислений) и сумматор, роль которого, выполняет метод ComputeOut.

TNeuronHopf, потомок TNeuron, реализует нейрон используемый в нейронной сети Хопфилда, единственным отличием от базового класса, является использования активационной функции в перекрытом методе ComputeOut.

Следующим порожденным классом, является TNeuronBP служащий для программной реализации многослойных нейронных сетей. Аббревиатура BP в имени класса не должна вводить вас в заблуждение, что нейрон этого типа используется исключительно в сетях обучаемых по алгоритму обратного распространения, этим, мы лишний раз хотели подчеркнуть, что в нашем случае нейронная сеть обучается по этому алгоритму.
Переписан метод ComputeOut, использующий теперь нелинейную активационную функцию, которая реализована в виде индексированного свойства процедурного типа OnActivationF. Кроме того, добавлены два важных свойства, Delta – содержащая локальную ошибку и индексированное свойство PrevUpdate – содержащее величину коррекции весовых коэффициентов на предыдущем шаге обучения сети.

Основным назначением базового класса TLayer и его потомков TLayerHopf и TLayerBP является объединение нейронов в слой, для упрощения работы с нейронами.

Компонент TNeuralNet базовый компонент для всех видов нейронных сетей. TNeuralNet обеспечивает необходимую функциональность производных компонентов. Этот компонент поддерживает методы для работы со слоями сети (AddLayer, DeleteLayer) и методы для манипуляций с исходными данными (AddPattern, DeletePattern, ResetPatterns). Метод Init служит для построения нейронной сети. Большинство методов объявленных в разделе public в базовом компоненте и его потомках – виртуальные, что позволяет легко перекрывать их.
Компонент TNeuralNetHopf реализует нейронную сеть Хопфилда.

Дополнительно включены следующие методы: InitWeights – запоминает предъявленные образцы в матрице образов и метод Calc – вычисляет выход сети Хопфилда.

Компонент TNeuralNetBP реализует многослойную нейронную сеть обучаемую по алгоритму обратного распространения ошибки.

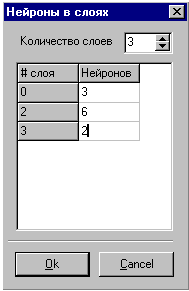
Дополнительно включены следующие методы: Compute – вычисляет выход нейронной сети, используется после обучения сети; TeachOffLine – обучает нейронную сеть. Компонент позволяет в режиме design-time, в окне Object Inspector, конструировать нейронную сеть добавляя или удаляя слои и нейроны в сети. Для этого используется редактор свойств NeuronsInLayer, имеющий следующий вид:

Коротко об искусственном нейроне

Чаще всего в подобных статьях начинают расписывать про устройство биологического нейрона, связь с его искусственной моделью и прочую лирику. Мы же этого делать не будем, а сразу перейдём к сути. Искусственный нейрон — это всего лишь взвешенная сумма значений входного вектора элементов, которая передаётся на нелинейную функцию активации f: z = f(y), где y = w·x + w₁·x₁ + . + w_{m – 1}·x_{m – 1} . Здесь w, . w_{m – 1} — коэффициенты, веса каждого элемента вектора, x, . x_{m – 1} — значения входного вектора X, y — взвешенная сумма элементов X, а z — результат применения функции активации. Мы вернёмся к функции активации немного позднее, а пока давайте придумаем, как вместо одного выходного значения получить n.

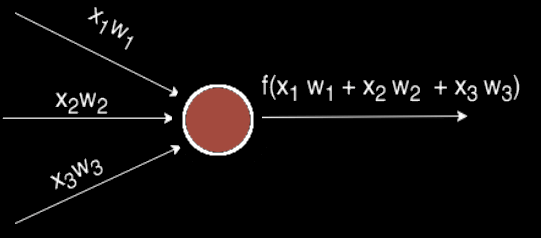
Вычисления, которые создают выходное значение, и в которых данные перемещаются слева направо на типовой схеме нейронной сети, составляют фрагмент «прямого распространения» работы системы. Вот код «прямого распространения»:

Первый цикл for позволяет нам проходить через несколько эпох. Внутри каждой эпохи, во втором цикле for , поочередно проходя по выборкам, мы вычисляем выходное значение для каждой выборки (то есть сигнал постактивации выходного узла). В третьем цикле for мы обращаемся индивидуально к каждому скрытому узлу, используя скалярное произведение для генерирования сигнала преактивации и функцию активации для генерирования сигнала постактивации.

После этого мы готовы вычислить сигнал преактивации для выходного узла (снова используя скалярное произведение), и мы применяем функцию активации для генерирования сигнала постактивации. Затем, чтобы вычислить итоговую ошибку, мы вычитаем целевое значение из значения полученного сигнала постактивации выходного узла.

Что такое нейронная сеть?

Большинство статей по нейронным сетям при их описании проводят параллели с мозгом. Мне проще описать нейронные сети как математическую функцию, которая отображает заданный вход в желаемый результат, не вникая в подробности.

Нейронные сети состоят из следующих компонентов:

• входной слой, x
• произвольное количество скрытых слоев
• выходной слой, ŷ
• набор весов и смещений между каждым слоем Wи b
• выбор функции активации для каждого скрытого слоя σ; в этой работе мы будем использовать функцию активации Sigmoid

На приведенной ниже диаграмме показана архитектура двухслойной нейронной сети (обратите внимание, что входной уровень обычно исключается при подсчете количества слоев в нейронной сети).

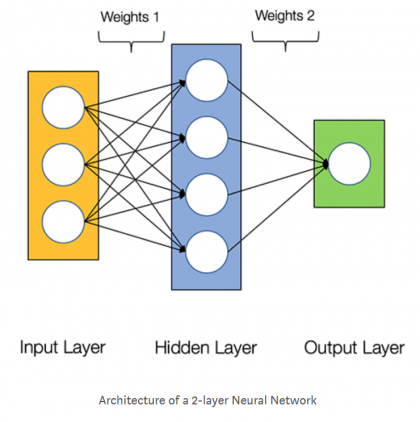
Создание класса Neural Network на Python выглядит просто:

Применение нейронной сети в распознавании изображений

Основой всех архитектур для видеонаблюдения является анализ, первой фазой которого будет распознавание изображения (объекта). Затем искусственный интеллект с помощью машинного обучения распознает действия и классифицирует их.

Для того чтобы распознать изображение, нейронная сеть должна быть прежде обучена на данных. Это очень похоже на нейронные связи в человеческом мозге — мы обладаем определенными знаниями, видим объект, анализируем его и идентифицируем.

Нейросети требовательны к размеру и качеству датасета, на котором она будет обучаться. Датасет можно загрузить из открытых источников или собрать самостоятельно

На практике означает, что до определённого предела чем больше скрытых слоев в нейронной сети, тем точнее будет распознано изображение. Как это реализуется?

Картинка разбивается на маленькие участки, вплоть до нескольких пикселей, каждый из которых будет входным нейроном. С помощью синапсов сигналы передаются от одного слоя к другому. Во время этого процесса сотни тысяч нейронов с миллионами параметров сравнивают полученные сигналы с уже обработанными данными.

Проще говоря, если мы просим машину распознать фотографию кошки, мы разобьем фото на маленькие кусочки и будем сравнивать эти слои с миллионами уже имеющихся изображений кошек, значения признаков которых сеть выучила.

В какой-то момент увеличение числа слоёв приводит к просто запоминанию выборки, а не обучению. Далее – за счёт хитрых архитектур.

Нейронные сети и байесовские модели

Две популярные парадигмы в области машинного обучения. Первые совершили настоящую революцию в области обработки больших объемов данных, дав начало новому направлению, получившему название глубинное обучение. Вторые традиционно применялись для обработки малых данных. Математический аппарат, разработанный в 2010 годы, позволяет конструировать масштабируемые байесовские модели. Это дает возможность применить механизмы байесовского вывода в современных нейронных сетях. Даже первые попытки построения гибридных нейробайесовских моделей приводят к неожиданным и интересным результатам. Например, благодаря использованию байесовского вывода в нейронных сетях удается сжать сеть приблизительно в 100 раз без потери точности ее работы.

Нейробайесовский подход потенциально может решить ряд открытых проблем в глубинном обучении: возможность катастрофического переобучения на шумы в данных, самоуверенность нейронной сети даже в ошибочных предсказаниях, неинтерпретируемость процесса принятия решения, уязвимость к враждебным атакам (adversarial attacks). Все эти проблемы осознаются научным сообществом, над их решением работают многие коллективы по всей планете, но готовых ответов пока нет.

Настроить

С TensorFlow 2 не за горами (не уверен, насколько далеко за этим углом задумано) создание вашей первой нейронной сети никогда не было проще (насколько TensorFlow идет).

Но что этоTensorFlow? Платформа машинного обучения (на самом деле Google?), Созданная и открытая из Google. Обратите внимание, что TensorFlow не является специальной библиотекой для создания нейронных сетей, хотя она в основном используется для этой цели.

Итак, что же нас ждет в TensorFlow 2?

TensorFlow 2.0 ориентирован на простоту и удобство использования, с такими обновлениями, как активное выполнение, интуитивно понятные высокоуровневые API и гибкое построение моделей на любой платформе.

Хорошо, давайте проверим эти претензии и установим TensorFlow 2:

Шаг 4. Создание своей нейросети

Читая разные статьи и руководства, вы так или иначе будете создавать небольшие нейросети. И это очень эффективно для обучения в целом.

Пример очень полезной информации можно найти здесь. В этом материале удивительное количество знаний сжато до 11 строк кода.

Прочитав вышеупомянутую статью и реализовав приведённые в ней примеры самостоятельно, вы закроете много пробелов в знаниях, а когда всё получится, почувствуете себя суперчеловеком)).

Что ещё? Ну, при реализации многих примеров используются векторные вычисления, поэтому понимание линейной алгебры тоже потребуется. Если же интересуют нейронные сети посложнее, то вот вам очередное руководство.

С его помощью вы сможете как написать свою нейросеть, так и поэкспериментировать с уже созданными сетями. Довольно забавным бывает найти нужный набор данных, а потом проверить разные предположения с помощью нескольких сетей.

Кстати, если интересуют хорошие наборы данных, вы можете посетить этот сайт.

Чем раньше вы начнёте свои эксперименты, тем лучше. Будет кстати и изучение Python-библиотек для программирования нейронных сетей: Theano, Lasagne, Nolearn. А ещё лучше — записаться на курс «Нейронные сети на Python» в OTUS. С его помощью вы освоите архитектуру нейронных сетей, узнаете методы их обучения и особенности реализации.